গাণিতিক গড়ের বৈশিষ্ট্য বা ধর্মাবলী

গাণিতিক গড় একটি গুরুত্বপূর্ণ কেন্দ্রীয় প্রবণতার পরিমাপ। এর বিভিন্ন বৈশিষ্ট্য বা ধর্ম রয়েছে, যা ডেটাসেট বিশ্লেষণের সময় গুরুত্বপূর্ণ ভূমিকা পালন করে। নিচে গাণিতিক গড়ের প্রধান বৈশিষ্ট্যগুলো দেওয়া হলো:

১. সহজ গণনা (Ease of Calculation):

গাণিতিক গড় সহজে গণনা করা যায়। ডেটাসেটের সকল মানের যোগফলকে ডেটার মোট সংখ্যার দ্বারা ভাগ করলেই গড় পাওয়া যায়।

২. প্রভাবিত হয় চরম মান দ্বারা (Affected by Extreme Values):

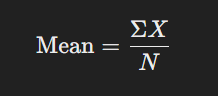
ডেটাসেটের মধ্যে কোনো চরম মান থাকলে গড় তার প্রভাব বহন করে। উদাহরণস্বরূপ, যদি কোনো ডেটাসেটে একটি অত্যন্ত বড় বা ছোট মান থাকে, তাহলে গড় তার দিকে ঝুঁকে পড়ে।

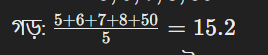
উদাহরণ:
ডেটাসেট: 5, 6, 7, 8, 50
গড়:
(৫০ এর কারণে গড় উচ্চতর হয়েছে।)

৩. প্রতিটি মানকে অন্তর্ভুক্ত করে (Considers Every Value):

গাণিতিক গড় প্রতিটি মানকে অন্তর্ভুক্ত করে, ফলে এটি পুরো ডেটাসেটের প্রতিনিধিত্ব করে।

৪. গাণিতিক গড় সর্বদা একক মান হয় (Single Value Representation):

গড় একটি একক মান হিসেবে ডেটাসেটকে উপস্থাপন করে, যা ডেটাসেটের সার্বিক বৈশিষ্ট্য নির্দেশ করে।

৫. বৈজ্ঞানিক বিশ্লেষণে গুরুত্বপূর্ণ (Useful in Mathematical Analysis):

গাণিতিক গড় বিভিন্ন বৈজ্ঞানিক এবং পরিসংখ্যানিক বিশ্লেষণে ব্যবহার করা হয়। এটি অন্যান্য পরিমাপের সাথে সহজেই সমন্বয় করা যায়।

৬. অতিসংবেদনশীল (Highly Sensitive):

ডেটাসেটে নতুন কোনো মান যোগ বা বিয়োগ করলে গড় তাৎক্ষণিকভাবে পরিবর্তিত হয়।

উদাহরণ:
ডেটাসেট: 10, 20, 30
গড়:
নতুন মান 40 যোগ করলে:
গড়:

৭. যথার্থতার সীমাবদ্ধতা (Limitations of Precision):

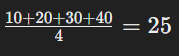
যদি ডেটার মান বিভাজক বা দশমিকের মাধ্যমে আসে, গড় প্রায়শই দশমিক আকারে থাকতে পারে।

৮. দ্বৈততা (Additive Property):

যদি একটি ডেটাসেট একাধিক উপগোষ্ঠীতে বিভক্ত হয়, তাহলে পুরো ডেটাসেটের গড় হলো উপগোষ্ঠীগুলোর গড়ের সমষ্টি।

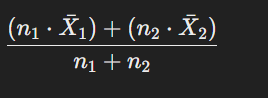
যেখানে,

৯. জ্যামিতিক বৈশিষ্ট্য (Geometric Property):

গাণিতিক গড় মানের যোগফলের বণ্টিত পরিমাণ নির্দেশ করে এবং এটি সরল বণ্টনের ক্ষেত্রে কার্যকর।

সারসংক্ষেপ

গাণিতিক গড় একটি গুরুত্বপূর্ণ পরিসংখ্যানিক মাপকাঠি যা ডেটাসেটের সার্বিক বৈশিষ্ট্য নির্দেশ করে। তবে এটি চরম মানের প্রতি সংবেদনশীল এবং সব পরিস্থিতিতে ব্যবহার উপযোগী নয়। সঠিক বিশ্লেষণের জন্য গাণিতিক গড়ের সীমাবদ্ধতাগুলো বোঝা প্রয়োজন।